Area Of A Circle Formula Proof

This is by no means a rigorous mathematical proof. It takes the subject of calculus to prove that this is actually the area of a circle. Grade 8 students are always amazed at how easy it is to find the area of rectilinear shapes compared with curved shapes.

Even in calculus, areas of curved forms are found through cutting them into smaller and smaller rectangles, trapezoids and triangles. The famous astronomer and mathematician Johannes Kepler found the volume of wine barrels by chopping them into smaller and smaller circles. We begin to discuss the area of the simplest curved shape, the circle, in Grade 7 but we don't actually discover the formula for the area of a circle until Grade 8.

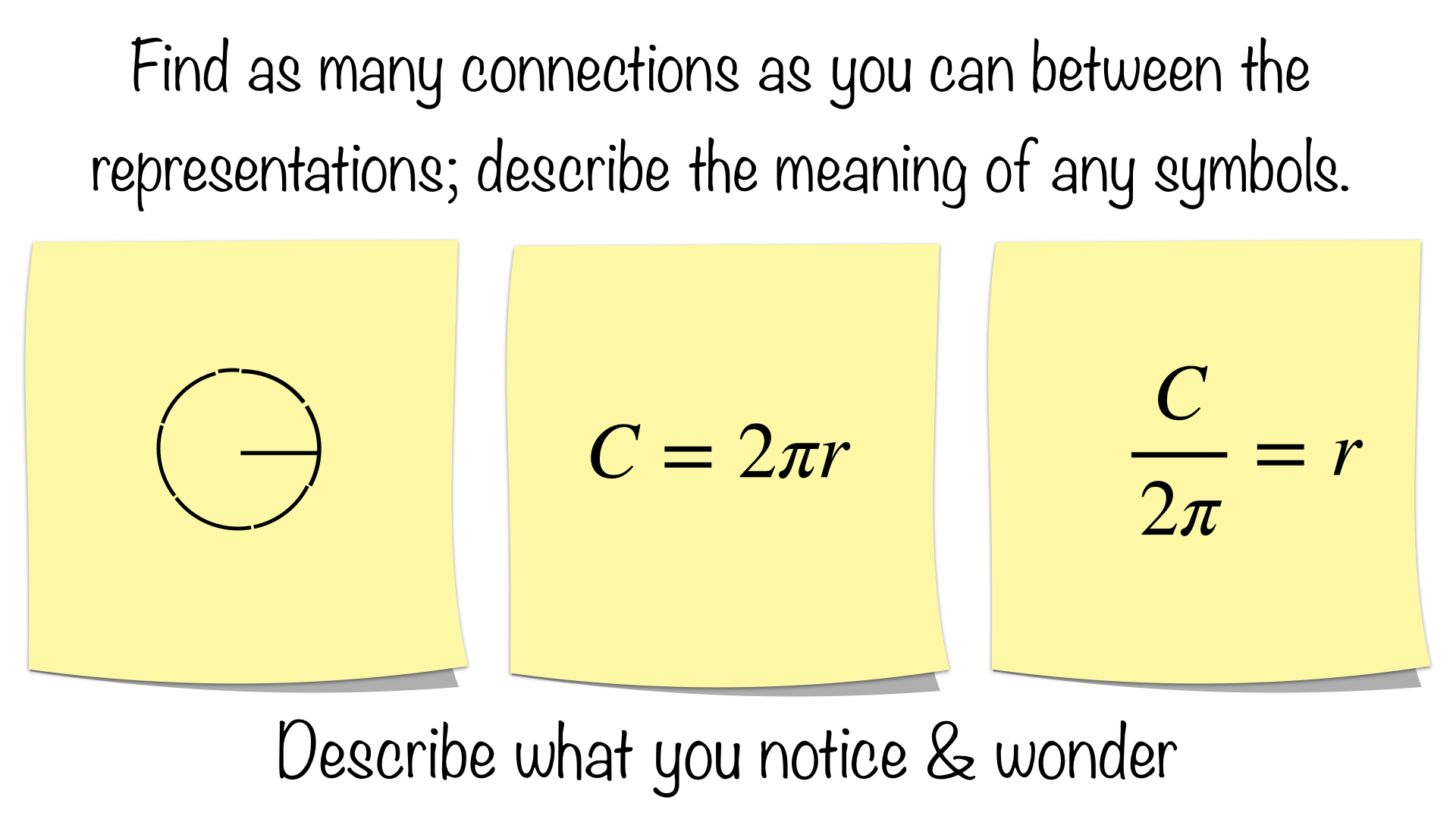
In the Grade 7 Geometry Main Lesson, the students discover irrational numbers like the golden ratio and pi. They discover pi by looking at the ratio of a circle's circumference to its diameter. In Grade 8, students are asked to complete an exercise in order to discover how one might find the area of a circle. They have previously discovered that the circumference of a circle is pi x the diameter or pi x twice the radius which plays a crucial role in this exercise.

They begin by cutting three equally sized circles out of paper into 4, 8 and 16 equal pieces respectively. The pieces are then reformed to create what ultimately begins to look like a rectangle. Pies, cakes, pizzas; so many foods we eat neatly lend themselves to mathematics, because they are models of circles. Bits cut off by connecting any two points on the circle are segments. Since both sectors and segments are part of a circle's interior, both have area. Why is the area of a circle pi times the square of the radius?

The usual definition of pi is the ratio of the circumference of a circle to its diameter, so that the circumference of a circle is pi times the diameter, or 2 pi times the radius. The animation above shows that a circle can be cut and rearranged to closely resemble a parallelogram of area pi times the square of the radius. By dividing the circle into more than eight slices, the approximation obtained in this manner would be even better.

Area Of A Circle Formula Derivation By dividing the circle into more and more slices, the approximating parallelograms approximate the area of the circle arbitrarily close. This give a geometric justification that the area of a circle really is "pi r squared". Dividing the rectangle into 1 x 1 squares allows us to visualize how many square units make up the area of the rectangle. If we multiply the base by the height of the above rectangle, we get an area of 18 square centimeters. By cutting up the rectangle, students can discover the formula of a rectangle or parallelogram on their own. From point B, on the circle, draw another circle with center at B, and radius OB.

The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii. Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. Fill the circle with radius r with concentric circles. After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle.

The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half.

If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r. A circle is a closed curve formed by a set of points on a plane that are the same distance from its center. The area of a circle is the region enclosed by the circle.

The area of a circle is equals to pi (π) multiplied by its radius squared. Angles are measured in degrees, but sometimes to make the mathematics simpler and elegant it's better to use radians which is another way of denoting an angle. A radian is the angle subtended by an arc of length equal to the radius of the circle.

( "Subtended" means produced by joining two lines from the end points of the arc to the center). For the right triangle in the above example, the circumscribed circle is simple to draw; its center can be found by measuring a distance of \(2.5\) units from \(A\) along \(\overline \). In the context of theways of knowing of TOK, the process of imagining an infinite number of circles relies heavily on visualisation and imagination. In practice we can never cut an infinite number of circles but we easily imagine doing this. This leap in imagination is what started calculus.

Medieval mathematicians of Europe were more versed in geometry than algebra given their resistance to the concept of zero and negative numbers . I can imagine that their preoccupation with geometry helped formulate calculus. Visual reasoning is often behind many breakthrough in mathematics and physics; therefore one can argue that reason and imagination are equally important for mathematics and the sciences. The fundamental theorem of calculus connects differentiation with integration.

Differentiation has been coveredpreviously and relies on taking a limit; this is a veryvisual process. Integration is also quite visual but involves approximating an area with strips, a limit is also taken, in this case the strip size is limited to zero. A circle is divided into concentric circles, and then opened up. The number of concentric circles increases everytime you press the button, can you figure out the the area of the strips?. If you ask someone how to calculate the area of the circle, they will give the answer πr2 as the area formula of the circle by heart. Of course, it states that the number of π is approximately 3, 3.14 or π depending on the school you are studying, department and course.

However, if the area of the circular segment is in question, not the whole circle, angles also come in between. A circle can be defined as a closed plane geometric shape. When it comes to technical terms, a circle can be defined as a locus of a point moving around a fixed point.

This is done at a fixed distance away from the central point. This means that the area of the circle is equal to the area that is enclosed within a closed curve with its outer line equidistant from the center. Also, the fixed distance from the center point is known as the radius of the circle. The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added.

The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that the area of a circle is proportional to the square of its radius. The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'. If the area of the circle is not equal to that of the triangle, then it must be either greater or less.

We eliminate each of these by contradiction, leaving equality as the only possibility. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center. The angle a circle subtends from its center is a full angle, equal to or radians.

A simple way to figure the area of a circle is to draw it on graph paper. The area of the circle would be approximately the number of squares inside the circle times the area of each square. This is only an approximation because the circumference of the circle cuts across some squares. You get a closer approximation if you count the number of partial squares as well as the number of complete squares inside the circle. Doing this leads to figuring out the value of pi rather easily.

We can also derive the value of the area of a triangle in a similar fashion. If we fill the circle with radius r with concentric circles and cut the circle along the indicated lines, then we will get a triangle after spreading the lines. A visual representation of this is available in the image that is mentioned below. We usually measure angles in degrees, for example, 90° in a right-angle, or 360° is a full revolution. This is mainly for historical reasons — the Babylonians used a base-60 number system and for example we still use 60 minutes in a degree.

Radian measure is crucial in later work on calculus. The idea is to define an angle so its size is the same as the size of the arc subtends it at the centre in a circle of unit radius. An alternative system is to measure angles in radians. Is made up of a large number of concentric circular pieces of very thin string. The sectors are pulled out of the circle and are arranged as shown in the middle diagram.

The length across the top is half of the circumference. When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area.

A perimeter of closed figures is defined as the length of its boundary. When it comes to circles, the perimeter is given using a different name. This circumference is the length of the boundary of the circle. If we open the circle to form a straight line, then the length of the straight line is the circumference. To define the circumference of the circle, knowledge of a term known as 'pi' is required.

The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius.

Students ultimately ask the question, how do we find the area of curvy shapes? Finding the area of any shape bounded by curves is actually quite complex. Because the concept of area comes from rectilinear shapes.

Digital technology is based on mathematics and curves, in the digital world, are just a collecting of very small squares called pixels. Dividing the rectangle in half allows us the find the area of a triangle . It becomes more difficult, however, to count up the squares that make up one of the triangles above. From this, we discover that it is easy to find the area of rectilinear shapes by simply dividing them into rectangles and triangles.

We can find the area of the trapezoid below, for example, without knowing the somewhat complicated trapezoid area formula. We simply divide the shape into a rectangle and two triangles. Students quickly learn and understand the concept of area when it comes to rectilinear forms . Multiplying the base by the height gives the area in square units. To prove this, let \(O\) be the center of the circumscribed circle for a triangle \(\triangle\,ABC \). Then \(O\) can be either inside, outside, or on the triangle, as in Figure 2.5.2 below.

In the first two cases, draw a perpendicular line segment from \(O\) to \(\overline\) at the point \(D \). The only asssumption made is that the circumference of the circle is 2πr. This can be demonstrated by measuring the radius and circumference of a number of different circles. The ratio of the circumference and the diameter is allways a constant value which is called π. There is no proof for the value of π ; it is fundamental constant of our universe.

Perhaps the value of π could be different in other parallel universes. It involves dividing the circle into many sectors and rearranging the sectors to form a rectangle. The base of the rectangle is shown to be πr and the height of the rectangle is r. The area of the rectangle is then the product of πr and r. The area of the circle which is equal to area of the rectangle is then πr2.

In this section, we will answer the question of what if the formula for the area of a circle. All students must know that any geometrical shape has its own area. The area can be defined as the region that is occupied by the shape in a two-dimensional plane. Circle is a closed two-dimensional figure which has a center where all the points in the plane are equidistant from it. Every line passing through the circle forms the line of reflection symmetry. In addition to this, it has rotational symmetry around the center for every angle.

Some of the examples of circles are wheels, pizzas, circular ground, etc. The first step is to approximate the area of a circle using a regular polygon. We inscribe a regular polygon in the circle and split up the polygon into congruent isosceles triangles as shown below. This is shown by the shaded region in the figure above. We then sum these slices between an angle of and . But, when using calculus, we do not use degrees, but rather we have to use radians, which as I explained in this blog, are a more natural unit for measuring an angle.